Question

You bought a new car for $28600 in 2010, and the value of the car depreciates by $400 each year.a) Find a formula for V, the value of the car, in terms of t, the number of years since 2010.V(t) =b) Find the value of the car in 201S.V(8) = $___

Answer 1

`\begin{gathered} V(t)=\text{ 28,600\lparen0.986\rparen}^t \\ V(8)\text{ = \$25,548.38} \end{gathered}`

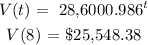
Step-by-step explanation

Given:

The price of a car in 2010 = $28,600

The cost of depreciation per year = $400

Desired Outcome:

1. V(t)

2. V(8)

Determine the depreciation rate

`\begin{gathered} rate\text{ = }(400)/(28600) \\ rate\text{ = 0.013986} \\ rate\text{ = 1.3986\%} \end{gathered}`

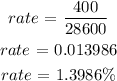
Applying the formula for decay

`V\text{ = A\lparen1-r\rparen}^n`

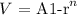
where

A = initial cost price

r = depreciation rate

n = number of years

So the formula for V(t)

`\begin{gathered} V(t)\text{ = 28,600\lparen1 - 0.013986\rparen}^t \\ V(t)\text{ = 28.600\lparen0.986\rparen}^t \end{gathered}`

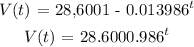
The value of the in 2018

`\begin{gathered} V(8)\text{ = 28,600\lparen0.986\rparen}^8 \\ V(8)\text{ = 28,600\lparen0.8933\rparen} \\ V(8)\text{ = 25,548.38} \end{gathered}`

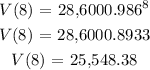
Hence, the formula for V(t) is 28,600(0.986)^t and the value of the car in 2018 is $25,548.38