ANSWER
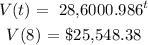
Step-by-step explanation
Given:
The price of a car in 2010 = $28,600
The cost of depreciation per year = $400
Desired Outcome:
1. V(t)
2. V(8)
Determine the depreciation rate
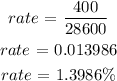
Applying the formula for decay
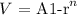
where
A = initial cost price
r = depreciation rate
n = number of years
So the formula for V(t)
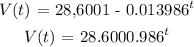
The value of the in 2018

Hence, the formula for V(t) is 28,600(0.986)^t and the value of the car in 2018 is $25,548.38