Answer:
• Increasing: (4, ∞)
,
• Decreasing: (-∞. 4)
,
• Constant: DNE
Explanation:
Given the function:
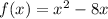
First, find the derivative:

When f'(x)<0:
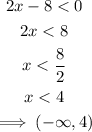
The interval of decrease is at (-∞, 4).
When f'(x)>0:

The interval of increase is at (4, ∞).
There is no interval at which the function is constant, so we write DNE.