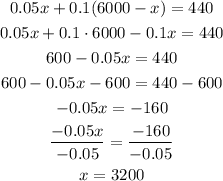Question

A college student earned $6000 during summer vacation working as a waiter in a popular restaurant.The student invested part of the money at 5% and the rest at 10%. If the student received a total of$440 in interest at the end of the year, how much was invested at 5%?

Answer 1

$3200

Explanation

Variables

• x: amount of money invested at 5%

,

• y: amount of money invested at 10%

The total amount of money invested is $6000, that is,

`x+y=6000\text{ \lparen eq. 1\rparen}`

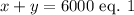
The interest, I, earned for an investment of P dollars at an interest rate of r in t years is calculated as follows:

`I=Prt`

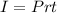
where r must be a decimal.

In the case of the amount of money invested at 5%, that is, r = 0.05 (=5/100), after t = 1 year, the interest is:

`I=x\cdot0.05\cdot1=0.05x`

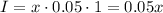
In the case of the amount of money invested at 10%, that is, r = 0.1 (=10/100), after t = 1 year, the interest is:

`I=y\cdot0.1\cdot1=0.1y`

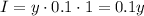
The student received a total of $440 in interest, then:

`0.05x+0.1y=440\text{ \lparen eq. 2\rparen}`

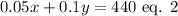
Isolating y from equation 1:

`\begin{gathered} x+y-x=6000-x \\ y=6000-x\text{ \lparen eq. 3\rparen} \end{gathered}`

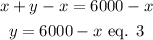
Substituting equation 3 into equation 2 and solving for x:

`\begin{gathered} 0.05x+0.1(6000-x)=440 \\ 0.05x+0.1\cdot6000-0.1x=440 \\ 600-0.05x=440 \\ 600-0.05x-600=440-600 \\ -0.05x=-160 \\ (-0.05x)/(-0.05)=(-160)/(-0.05) \\ x=3200 \end{gathered}`