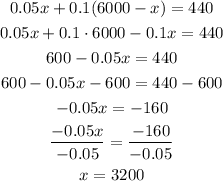Answer
$3200
Explanation
Variables
• x: amount of money invested at 5%
,
• y: amount of money invested at 10%
The total amount of money invested is $6000, that is,
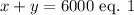
The interest, I, earned for an investment of P dollars at an interest rate of r in t years is calculated as follows:
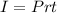
where r must be a decimal.
In the case of the amount of money invested at 5%, that is, r = 0.05 (=5/100), after t = 1 year, the interest is:
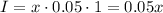
In the case of the amount of money invested at 10%, that is, r = 0.1 (=10/100), after t = 1 year, the interest is:
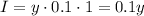
The student received a total of $440 in interest, then:
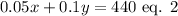
Isolating y from equation 1:

Substituting equation 3 into equation 2 and solving for x: