Question

The right side of a tower has a shape that can be approximated by the graph of the function defined byf(x)=-304 In x/208Answer parts (a) through (c)(will post parts b and c as they appear)(a) Explain why the shape of the left side of the tower has the formula given by f(-x)(b) the short horizontal line at the top of the figure has length 16.3056 feet. approximately how tall is the tower?(c) approximately how far from the center of the tower is the point on the right side that is 450 feet above the ground?

Answer 1

Part A

The shape of the figure is symmetric about the y-axis. Therefore we can express the left hand side as the function f(-x)

Part B

We have the data of the upper part of the figure.

First let's calculate the value of the corresponding x-coordinate

In this case

x = 16.3056/2

x = 8.1528

Now that we know the value of x we can evaluate it in the function f(x) and then know the height of the tower.

`\begin{gathered} f(x)=-304\cdot\ln ((8.1528)/(208)) \\ f(x)=984.70 \end{gathered}`

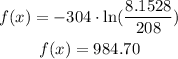
The height of the tower would equal 984.70 ft.

Part C

We have information on the height of the point that is f(x) = 450

Now let's calculate the value for x

`\begin{gathered} f(x)=450 \\ -304\cdot\ln ((x)/(208))=450 \\ \ln ((x)/(208))=(450)/(-304) \\ \ln ((x)/(208))=-1.480 \\ x=208e^(-1.408) \\ x=50.883 \end{gathered}`

The point would be a total of 50,883 from the centre of the tower.