Question

The profit in dollars generated by producing and selling n bicycles per week is given by the formula P(n)=−5n2+400n−6000. What is the minimum number of bicycles that must be produced and sold to break even?

Answer 1

Answer:

The minimum number of bicycles that must be produced and sold to break even = 20

Step-by-step explanation:

The profit generated by producing and selling n bicycles per week is given by the formula:

`P(n)=-5n^2+400n-6000`

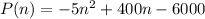
To get the minimum number of bicycles that must be produced and sold to break even, let P(n) = 0 (Since break even means no profit is made)

`\begin{gathered} 0=-5n^2+400n-6000 \\ 5n^2-400n+6000=0 \end{gathered}`

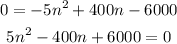
Solve the resulting quadratic equation above

`\begin{gathered} 5n^2-300n-100n+6000=0 \\ 5n(n-60)-100(n-60)=0 \\ (5n-100)(n-60)=0 \\ 5n-100=0 \\ 5n=100 \\ n=(100)/(5) \\ n=20 \\ n-60=0 \\ n=60 \end{gathered}`

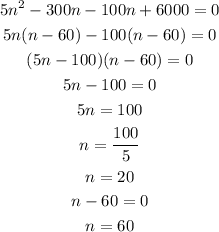
This means that, to break even, either 60 or 20 bicycles must be produced and sold

The minimum number of bicycles that must be produced and sold to break even = 20