Question

I’m just wanting to know how to get to the answers to these questions

Answer 1

Given:

`f(x)=(5)/(x),x_0=1,x_n=9`

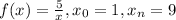
Step-by-step explanation:

To find: The area when n = 2 (since, 2 rectangles)

Finding the given change in x,

`\begin{gathered} \Delta x=(b-a)/(n) \\ =(9-1)/(2) \\ =4 \end{gathered}`

Defining the partition intervals,

`x:\lbrace(1,5),(5,9)\rbrace`

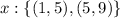
Choose the midpoint in each interval,

`x_m=\lbrace3,7\rbrace`

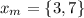
Finding the value of the function at the point,

`\begin{gathered} f(3)=(5)/(3) \\ f(3)\approx1.6667 \\ f(7)=(5)/(7) \\ f(7)\approx0.7143 \end{gathered}`

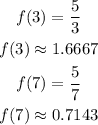
Using the midpoint formula,

`\begin{gathered} A=\Delta x(f(x_(m_1))+f(x_(m_2))) \\ =4(1.6667+0.7143) \\ A\approx9.5238\text{ square units} \end{gathered}`

Final answer: The area under 2 rectangles is 9.5238 square units.

To find: The area when n = 4 (4 rectangles)

Finding the given change in x,

`\begin{gathered} \Delta x=(b-a)/(n) \\ =(9-1)/(4) \\ =2 \end{gathered}`

Defining the partition intervals,

`x:\lbrace(1,3),(3,5),(5,7),(5,9)\rbrace`

Choose the midpoint in each interval,

`x_m=\lbrace2,4,6,8\rbrace`

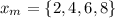
Finding the value of the function at the point,

Using the midpoint formula,

`\begin{gathered} A=\Delta x(f(x_(m_1))+f(x_(m_2))+f(x_(m_3))+f(x_(m_4))) \\ =2(2.5+1.25+0.833+0.625) \\ =2(5.2083) \\ A\approx10.4167\text{ square units} \end{gathered}`

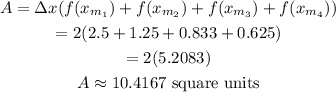
Final answer: The area under 4 rectangles is 10.4167 square units.