Given data:
* The initial velocity of the train is 30 m/s.
* The time taken by the train is 44 s.
* The final velocity of the train is zero.
Solution:
(a). By the kinematics equation,
The acceleration of the train in terms of the change in velocity is,
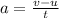
where v is the final velocity, u is the initial velocity, and t is the time taken by the train to stop,
Substituting the known values,
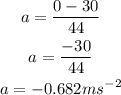
Here, the negative sign indicates the decrease in the velocity with time,
Thus, the accerlation of the train is -0.682 meter per second squared.
(b). By the kinematics equation, the distance tarveled by the train is,
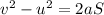
where S is the distance traveled by the train,
Substituting the known values,
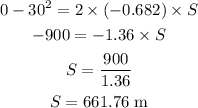
Thus, the stopping distance is 661.76 m.