Given the equation of the line AB:
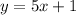
You can identify that it is written in Slope-Intercept Form:

Where "m" is the slope of the line and "b" is the y-intercept.
Notice that the slope of the line AB is:
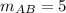
And its y-intercept is:
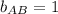
By definition, parallel lines have the same slope but different y-intercepts. Therefore, you can determine that the slope of the line parallel to line AB is:
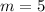
You know that it contains the point:
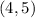
Therefore, you can substitute the slope and the coordinates of that point into this equation:

And then solve for "b", in order to find the y-intercept:

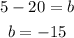
Therefore, you get that the equation of this line in Slope-Intercept Form is:
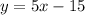
Hence, the answer is: Last option.