Question

Use the factorial notation to find the first four terms of the sequence whose general term is given below. If your answer is not an integer type it as a reduced fraction a_n = \frac{4}{n!} 1st term = Answer2nd term = Answer3rd term = Answer4th term = Answer

Answer 1

Case: Sequence with factorial notation

A sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called elements, or terms). The number of elements (possibly infinite) is called the length of the sequence.

Given:

`a_n=\text{ }(4)/(n!)`

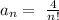
Required: To find the first 4 terms

Method:

First term, n=1

`\begin{gathered} a_(n)=\text{(4)/(n!)} \\ a_1=\frac{\text{4}}{1\text{!}} \\ a_1=\frac{\text{4}}{1} \\ a_1=\text{4} \end{gathered}`

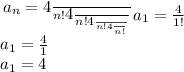
Second term, n= 2

`\begin{gathered} a_2=\frac{\text{4}}{2!} \\ a_2=\frac{\text{4}}{2*1} \\ a_2=\frac{\text{4}}{2} \\ a_2=2 \end{gathered}`

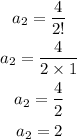
Third term, n =3

`\begin{gathered} a_3=\frac{\text{4}}{3!} \\ a_3=\frac{\text{4}}{3*2*1} \\ a_3=(2)/(3) \end{gathered}`

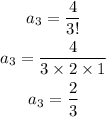
Fourth term, n= 4

`\begin{gathered} a_4=\frac{\text{4}}{4!} \\ a_4=\frac{\text{4}}{4*3*2*1} \\ a_4=(1)/(6) \end{gathered}`

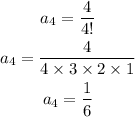
Final answer:

First term, a= 4

Second term, a= 2

Third term, a= 2/3

Fourth term: a= 1/6