Question

1

What is the pH of a substance that has a hydrogen ion concentration of 1.2 x10-2 M2
ZpG

Answer 1

Approximately
`1.92`.

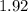Step-by-step explanation:

The
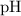`{\rm pH}` of a solution is the opposite of the base-
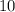`10` logarithm of that solution's
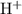`{\rm H^(+)}` concentration measured in
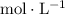`{\rm mol \cdot L^(-1)}`. In other words:

`{\rm pH} = - \log_(10) ([{\rm H^(+)])`.

Using properties of logarithms:

`\begin{aligned}{\rm pH} &= - \log_(10) ([{\rm H^(+)]) \\ &= -\left(\frac{\ln([{\rm H^(+)]})}{\ln(10)}\right)\end{aligned}`.

In this question,
`[{\rm H^(+)}] = 1.2 * 10^(-2)\; {\rm mol \cdot L^(-1)}`. Therefore:

`\begin{aligned}{\rm pH} &= - \log_(10) ([{\rm H^(+)]) \\ &= -\left(\frac{\ln([{\rm H^(+)]})}{\ln(10)}\right) \\ &= - (\ln(1.2 * 10^(-2)))/(\ln(10)) \\ &\approx 1.92\end{aligned}`.

By convention, the number of decimal values in the
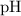`{\rm pH}` should be equal to the number of significant figures in the
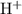`{\rm H^(+)}` concentration of the solution.

In this question, there are two significant figures in the measurement
`[{\rm H^(+)}] = 1.2 * 10^(-2)\; {\rm mol \cdot L^(-1)}`. Thus, the
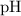`{\rm pH}` result should be rounded to two decimal places.