Answer:
C) the x-intercepts: (-3, 0) and (5, 0); y-intercept (0, -15)
Step-by-step explanation:
The y-intercept of the function is the value of f(x) when x is equal to 0, so if we replace x by 0, we get:
f(x) = x² - 2x - 15
f(0) = 0² - 2(0) - 15
f(0) = 0 - 0 - 15
f(0) = -15
Therefore, the y-intercept is the point (0, -15)
On the other hand, the x-intercepts are the values of x when f(x) is equal to zero. So, to find the x-intercepts, we need to solve the following equation:
f(x) = x² - 2x - 15 = 0
x² - 2x - 15 = 0
So, if we factorize the expression we get:
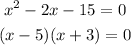
Then, there are two possible options:
x - 5 = 0
x - 5 + 5 = 0 + 5
x = 5
Or
x + 3 = 0
x + 3 - 3 = 0 - 3
x = - 3
Therefore, the x-intercepts of the equation are the points (-3, 0) and (5, 0)
So, the answer is C) the x-intercepts: (-3, 0) and (5, 0); y-intercept (0, -15)