Question

The half life of Radium-226 is 1590 years. If a sample contains 200 mg, how many mg will remain after 4000 years?

Answer 1

We know that

• The initial mass is 200 mg.

,

• The time is 4000 years.

,

• The half-life is 1590 years.

Let's use the half-life formula.

`N(t)=N_o(0.5)^{\frac{t}{u_{}}}`

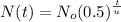
Using the given magnitudes, we have the following

`N(4000)=200\cdot(0.5)^{(4000)/(1590)}\approx35mg`

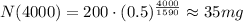
Therefore, after 4000 years, there will remain 35 mg of Radium-226.