We know that
• The initial mass is 200 mg.
,
• The time is 4000 years.
,
• The half-life is 1590 years.
Let's use the half-life formula.
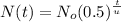
Using the given magnitudes, we have the following
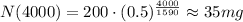
Therefore, after 4000 years, there will remain 35 mg of Radium-226.