Question

X^4-3x^3-13x^2+27x+36 given x - 4 is a factorGraph the polynomial.

Answer 1

Let's first determine the zeros of the given polynomial:

`x^4-3x^3-13x^2+27x+36`

One of the factors is given, x - 4.

To summarize, the factors are:

`x^4-3x^3-13x^2+27x+36\text{ = }\mleft(x+1\mright)\mleft(x+3\mright)\mleft(x-3\mright)\mleft(x-4\mright)`

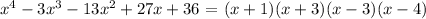
This polynomial is a positive even power (in particular, it's of degree four), so the graph will go up on both ends.

So the zeroes (that is, the x-intercepts (at y = 0)) are at:

x = -1, -3, 3, 4

If we plot a few other points on our T-chart, it will be no trouble to do the graph. Because the pairs of x-intercepts are so close, I'll go to the trouble of evaluating the polynomial at the halfway points between the zeroes; that is, at x = -2 and x = 3.5.

This polynomial is a fourth power, so it likely grows quickly. So I'll do one point below and another above the zeroes.

Substituting the given equation by a number of possible x - values.

x x^4-3x^3-13x^2+27x+36 = y

-4 168

-2 -30

0 36

3.5 -7.3125

5 96

Plotting the graph will be: