Question

Use the graph of the function to find the domain and range of F. Use the graph to find the indicated function value. (Question is in the photo sorry lol)

Answer 1

Step-by-step explanation

Calculus / Functions / Graphs and Functions / Domain and Range of a Function

In this problem, we have the graph of a function, and we must determine the domain, range and the values of the functions for different values of x.

(1) Domain

The domain of a function is the complete set of possible values of the independent variable (x, usually).

Looking at the graph, we see that the independent variable x takes all the values of the real line, from -∞ to +∞. So the domain of the function is:

`Domain=(-\infty,\infty).`

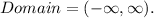
(2) Range

The range of a function is the complete set of all possible resulting values of the dependent variable (y, usually) after we have substituted the domain.

Looking at the graph, we see that the dependent variable y takes all the values:

`y>-3.`

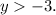
So the range of the function is:

`Range=(-3,\infty).`

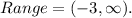
(3) Looking at the graph, we find the following values of the function:

• (a), For x = 2 we have f(2) = 0,

,

• (b), For x = 1 we have f(1) = 1,

,

• (c), For x = 3 we have f(3) = 3,

,

• (d) For x = -1 we have f(-1) = 3.

Answer

Domain = (-∞, ∞)

Range = (-3, ∞)

(a) f(2) = 0

(b) f(1) = 1

(c) f(3) = 3

(d) f(-1) = 3