Question

Find Sine, Cosine, and Tangent for angle A below: SIMPLIFY THE FRACTIONS B. 12 16 20 C sinA= COSA = tanA=

Answer 1

Sin A = 16/20

Cos B = 12/20

tan A =16/12

Step-by-step explanation:

sin is defined as

`\sin A=(opposite)/(hypotenuse)`

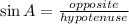
Now the side opposite to angle A measures 16 and the hypotenuse measures 20; therefore,

`\sin A=(16)/(20)`

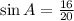
Similarly,

`\cos A=\frac{\text{adjacent}}{hypotenuse}`

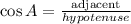
since for angle A adjacent = 12 and hypotenuse = 20, the above gives

`\cos A=(12)/(20)`

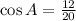
Finally, the tangent ratio gives

`\tan A=(opposite)/(adjacent)`

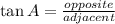
since opposite = 16 and adjacent = 12, the above gives

`\tan A=(16)/(12)`

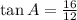
Hence, to summerize ur results