Question

Two containers designed to hold water are side by side, both in the shape of acylinder. Container A has a diameter of 24 feet and a height of 14 feet. Container Bhas a diameter of 16 feet and a height of 16 feet. Container A is full of water and thewater is pumped into Container B until Containter B is completely full.To the nearest tenth, what is the percent of Container A that is empty after thepumping is complete?playContainer AContainer Bd-1616h-14

Answer 1

Concept

`\begin{gathered} \text{The volume of a cylinder = }\pi r^2h \\ \pi\text{ = 3.14} \end{gathered}`

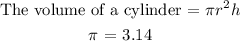
r = radius

h = height

Step 1: Find the radius of both A and B

Radius of A r = 24/2 = 12 feet

Radius of B = 16/2 = 8 feet

Step 2: Find the volume of A and B

`\begin{gathered} \text{Given data} \\ A \\ r\text{ = 12} \\ h\text{ = 14} \\ \text{Volume = }\pi r^2h \\ =\text{ 3.14 }*12^2\text{ }*\text{ 14} \\ =6330.24ft^3 \end{gathered}`
`\begin{gathered} B \\ r\text{ = 8} \\ h\text{ = 16} \\ \text{Volume = }\pi r^2h \\ =\text{ 3.14 }*8^2\text{ }*\text{ 16} \\ =3215.36ft^3 \end{gathered}`

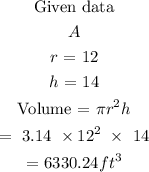
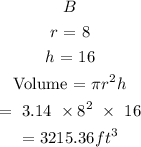
Step 3: To find the percentage of container A that is empty after the pumping is complete, you find the volume of space in the container A

Volume of space in container A = Volume of water pumped into B = 3215.36

Step 4: percent of Container A that is empty after the pumping is complete

`\begin{gathered} \text{Percent of container A that is empty after pumping is complete } \\ =\text{ }(3215.36)/(6330.24)\text{ }*\text{ 100\%} \\ =\text{ }(321536)/(6330.24) \\ =\text{ 50.79\%} \end{gathered}`

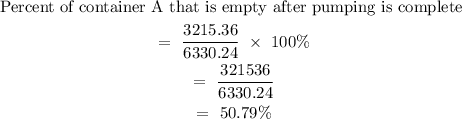
Final answer

= 50.8%