Concept
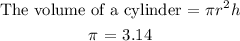
r = radius
h = height
Step 1: Find the radius of both A and B
Radius of A r = 24/2 = 12 feet
Radius of B = 16/2 = 8 feet
Step 2: Find the volume of A and B
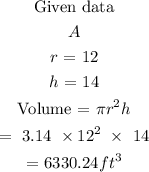

Step 3: To find the percentage of container A that is empty after the pumping is complete, you find the volume of space in the container A
Volume of space in container A = Volume of water pumped into B = 3215.36
Step 4: percent of Container A that is empty after the pumping is complete

Final answer
= 50.8%