Question

How do you find the diagonal intersection? I already started the process with a tutor but my phone acted up and it exited the session.

Answer 1

7)

In order to classify the quadrilateral BCDE, let's find the slope of all four sides.

The slope 'm' of two points (x1, y1) and (x2, y2) is calculated as:

`m=(y_2-y_1)/(x_2-x_1)`

So using the four pairs of points, we have:

`\begin{gathered} B(-6,5),C(6,2)\colon \\ m=(2-5)/(6-(-6))=-(3)/(12)=-(1)/(4) \\ \\ C(6,2),D(2,-9)\colon \\ m=(-9-2)/(2-6)=-(11)/(-4)=(11)/(4) \\ \\ D(2,-9),E(-10,-6)\colon_{} \\ m=(-6-(-9))/(-10-2)=(3)/(-12)=-(1)/(4) \\ \\ E(-10,-6),B(-6,5)\colon \\ m=(5-(-6))/(-6-(-10))=(11)/(4) \end{gathered}`

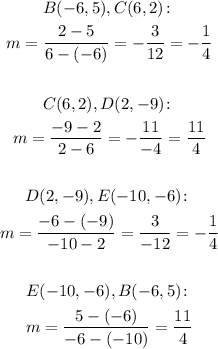
We can see that we have two pairs of parallel slopes, so we have a parallelogram.

In order to find if the angles are 90°, the sides need to be perpendicular, so the slopes need to relate as follows:

`m_1=-(1)/(m_2)`

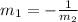
We don't have this relation with the slopes we calculated, so the angles are not right angles. So the quadrilateral BCDE is a parallelogram.

8)

In a parallelogram, the diagonals intersect in their middle point, so the coordinates of the intersection point 'M' are the average of the starting and ending point.

So we have that:

`\begin{gathered} B(-6,5),D(2,-9)\colon \\ M=((-6+2)/(2),(5-9)/(2))=(-(4)/(2),-(4)/(2))=(-2,-2) \\ \\ C(6,2),E(-10,-6)\colon \\ M=((6-10)/(2),(2-6)/(2))=(-(4)/(2),-(4)/(2))=(-2,-2) \end{gathered}`

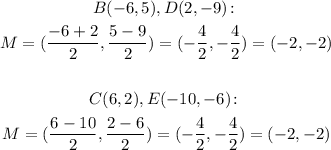
So the coordinates of the intersection point are (-2, -2).