7)
In order to classify the quadrilateral BCDE, let's find the slope of all four sides.
The slope 'm' of two points (x1, y1) and (x2, y2) is calculated as:
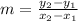
So using the four pairs of points, we have:
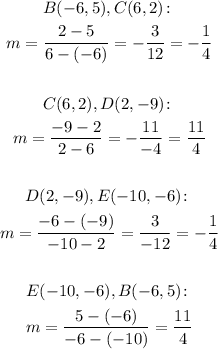
We can see that we have two pairs of parallel slopes, so we have a parallelogram.
In order to find if the angles are 90°, the sides need to be perpendicular, so the slopes need to relate as follows:
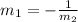
We don't have this relation with the slopes we calculated, so the angles are not right angles. So the quadrilateral BCDE is a parallelogram.
8)
In a parallelogram, the diagonals intersect in their middle point, so the coordinates of the intersection point 'M' are the average of the starting and ending point.
So we have that:
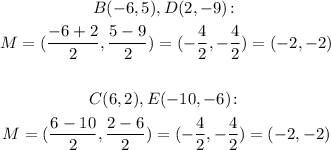
So the coordinates of the intersection point are (-2, -2).