ANSWER
s = 7.38
Step-by-step explanation
The standard deviation, s, of a sample is the square root of the variance, s²,
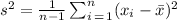
Where n is the number of data, 5, and x with the line on top is the mean,
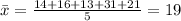
So the variance is,
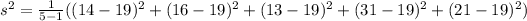
Solve the subtractions,
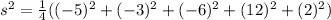
Solve the squares, add and divide by 4,
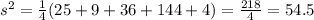
Finally, to find the standard deviation, take the square root,
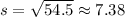
Hence, the standard deviation is 7.38, rounded to the nearest hundredth.