Given the initial value of the car at $22,000 and the annual depreciation value at 35%. To calculate the resale value of the car after a given number of years, we shall apply the exponential decay formula;
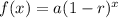
This can also be written as;
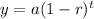
The value of x in the first equation is the same as the value of t in the second equation. x is the number of years, and t is also the same, the number of years.
Therefore, with the values already given, we would have;
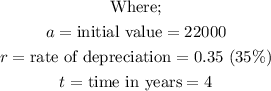
The resale value after 4 years would now be;
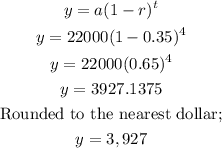
ANSWER:
The resale value after 4 years would be $3,927