Question

Solving a word problem using a quadratic equation with irration...EspanolA ball is thrown from a height of 61 meters with an initial downward velocity of 6 m/s. The ball's height h (in meters) after t seconds is given by the following.h=61-6-57How long after the ball is thrown does it hit the ground?Round your answer(s) to the nearest hundredth.(If there is more than one answer, use the "or" button.)

Answer 1

The ball's heigh h after t seconds given by the following cuadratic function:

`h(t)=61-6t-5t^2`

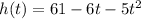
Q) The question asks about time required for the ball to hit the ground.

A) When the ball hits the ground, the value of fuction h(t) is equal to zero. So we want to solve for t the following equation:

`h(t)=61-6t-5t^2=0`

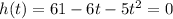
That's mean that we want to find the roots of a polynomial of order two.

The roots of a second order polynomial of the general form:

`p(t)=a\cdot t^2+b\cdot t+c`

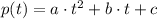
can be calculated using the following formula:

`t_{}=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a}`

Now, we want to use the last formula to find the values of t. In order to that we must know first the values of a, b and c.

Comparing the general formula of a polynomial of second order p(t) with our polynomial of second order h(t) we see that:

`\begin{gathered} a=-5 \\ b=-6 \\ c=61 \end{gathered}`

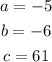
Now, we can replace those numbers in the formula for t. Doing that we find that the roots of the polynomial are:

`\begin{gathered} t=\frac{-(-6)\pm\sqrt[]{(-6)^2-4\cdot(-5)\cdot61}}{2\cdot(-5)} \\ t=\frac{6\pm\sqrt[]{1256}}{-10} \\ t_1\cong-4.14 \\ t_2\cong2.94 \end{gathered}`

Now, we see that we have two solutions!

Usually, because this is a problem with a physical interpretation, the only correct solution is the positive one. That's becase only a positive time means a moment in the future, what we are trying to predict, a negative time means a moment in the past.

Answer

- The two mathematical correct solutions are:

t1 = -4.14

t2 = 2.94

- The only physical solution is:

t2 = 2.94