Question

solve the system of equations. find both X's and multiply them together for the answer you enter. y=6x+1y=2x^2-10x-2

Answer 1

The given system of equations is:

`\begin{gathered} y=6x+1\text{ Eq.(1)} \\ y=2x^2-10x-2\text{ Eq.(2)} \end{gathered}`

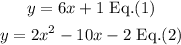
As y=y then we can equal both equations and solve for x as follows:

`\begin{gathered} y=y \\ 6x+1=2x^2-10x-2 \\ \text{Subtract 6x from both sides} \\ 6x+1-6x=2x^2-10x-2-6x \\ 1=2x^2-16x-2 \\ \text{Subtract 1 from both sides} \\ 1-1=2x^2-16x-2-1 \\ 0=2x^2-16x-3 \end{gathered}`

Now, we have an equation in the form:

`ax^2+bx+c=0^{}`

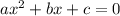
Where a=2, b=-16 and c=-3, we can apply the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Replace the a, b and c values and solve to find the x-values:

`\begin{gathered} x=\frac{-(-16)\pm\sqrt[]{(-16)^2-4(2)(-3)}}{2(2)} \\ x=\frac{16\pm\sqrt[]{256+24}}{4} \\ x=\frac{16\pm\sqrt[]{280}}{4} \\ x=\frac{16\pm\sqrt[]{4\cdot70}}{4} \\ x=\frac{16\pm2\sqrt[]{70}}{4} \\ \text{Then:} \\ x1=\frac{16+2\sqrt[]{70}}{4}=(16)/(4)+\frac{2\sqrt[]{70}}{4}=4+4.18=8.18 \\ x2=\frac{16-2\sqrt[]{70}}{4}=(16)/(4)-\frac{2\sqrt[]{70}}{4}=4-4.18=-0.18 \end{gathered}`

Then the x-values are: 8.18 and -0.18, and its multiplication is:

`8.18\cdot-0.18=-1.5`

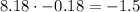
Answer: -1.5