The given system of equations is:
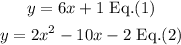
As y=y then we can equal both equations and solve for x as follows:

Now, we have an equation in the form:

Where a=2, b=-16 and c=-3, we can apply the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Replace the a, b and c values and solve to find the x-values:
![\begin{gathered} x=\frac{-(-16)\pm\sqrt[]{(-16)^2-4(2)(-3)}}{2(2)} \\ x=\frac{16\pm\sqrt[]{256+24}}{4} \\ x=\frac{16\pm\sqrt[]{280}}{4} \\ x=\frac{16\pm\sqrt[]{4\cdot70}}{4} \\ x=\frac{16\pm2\sqrt[]{70}}{4} \\ \text{Then:} \\ x1=\frac{16+2\sqrt[]{70}}{4}=(16)/(4)+\frac{2\sqrt[]{70}}{4}=4+4.18=8.18 \\ x2=\frac{16-2\sqrt[]{70}}{4}=(16)/(4)-\frac{2\sqrt[]{70}}{4}=4-4.18=-0.18 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9zckgtn66bvnheqmrlo44k7vo2cmky11jb.png)
Then the x-values are: 8.18 and -0.18, and its multiplication is:

Answer: -1.5