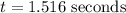To answer this question we will set and solve an equation.
Since the height of the ball above the ground after t seconds is:
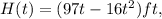
then its velocity after t seconds is:
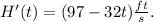
Setting H'(t)=48.5ft/s we get:
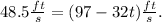
Therefore:
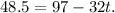
Subtracting 97 from the above equation we get:
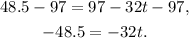
Dividing the above equation by -32 we get:
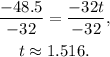
Answer: