Question

A ball is kicked from a height of 3 feet above the ground. The height of the ball, h(t), is given byh(t) = -5t2 + 14t +3, where t is the time in seconds after the ball is kicked. How long will it take theball to hit the ground after it is kicked?

Answer 1

Let:

`h(t)=-5t^2+14t+3`

We need to know when:

`h(t)=0`

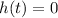
so:

`\begin{gathered} -5t^2+14t+3=0 \\ -(5t^2-14t-3)=0 \end{gathered}`

The coefficient of t² is 5 and the constant term is -3. The product of 5 and -3 is -15, the factors of -15 which sum to -14 are 1 and -15. so:

`\begin{gathered} 5t^2-14t-3=(t-3)(5t+1) \\ so\colon \\ -(5t^2-14t-3)=-(t-3)(5t+1) \end{gathered}`

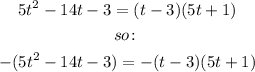
Therefore:

`\begin{gathered} t=-(1)/(5) \\ t=3 \end{gathered}`

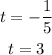
Since -1/5 s wouldn't make any sense, the answer is:

t = 3 seconds