Composite Function
The composite function named
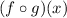
is defined as:
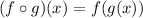
We are given the functions:
![f(x)=\frac{1}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/g5dcsrpej58rxavux9l6zde8edbzz0r0vb.png)
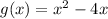
The composite function is obtained by substituting g into f as follows:
![(f\circ g)(x)=\frac{1}{\sqrt[]{x^2-4x}\text{ }}](https://img.qammunity.org/2023/formulas/mathematics/college/v3xis05gd8f5sh8hw98m646z81nfog2wsl.png)
We are required to find the domain of the composite function.
Since it's a rational function, the denominator cannot be 0, thus:
![\sqrt[]{x^2-4x}\text{ }\\e0](https://img.qammunity.org/2023/formulas/mathematics/college/u9c6z2m2hy882clr5lbwjmiz3rtm1lmt27.png)
The radicand of a square root must be non-negative:
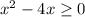
But we must exclude 0 from the solution, thus the inequality to solve is:
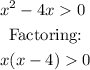
The product of x and x-4 must be positive. It can only happen when both are positive OR both are negative, thus:
x > 0
x - 4 > 0 => x > 4
The and combination of these conditions is (4,∞)
Now for the second condition:
x < 0
x - 4 < 0 => x < 4
The and combination of these conditions is (-∞,0)
The or combination of the solutions above is:
Solution: (-∞,0) U (4,∞)