1 Answer

Mohammad Raheem · Answer 1 · 2023-01-13T06:53:12+0000

Composite Function

The composite function named

$(f\circ g)(x)$

is defined as:

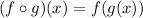
$(f\circ g)(x)=f(g(x))$

We are given the functions:

$f(x)=\frac{1}{\sqrt[]{x}}$
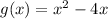
g(x)=x^2-4x

The composite function is obtained by substituting g into f as follows:

$(f\circ g)(x)=\frac{1}{\sqrt[]{x^2-4x}\text{ }}$

We are required to find the domain of the composite function.

Since it's a rational function, the denominator cannot be 0, thus:

$\sqrt[]{x^2-4x}\text{ }\\e0$

The radicand of a square root must be non-negative:

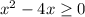
$x^2-4x\ge0\text{ }$

But we must exclude 0 from the solution, thus the inequality to solve is:

$\begin{gathered} x^2-4x>0\text{ } \\ \text{Factoring:} \\ x(x-4)>0 \end{gathered}$

The product of x and x-4 must be positive. It can only happen when both are positive OR both are negative, thus:

x > 0

x - 4 > 0 => x > 4

The and combination of these conditions is (4,∞)

Now for the second condition:

x < 0

x - 4 < 0 => x < 4

The and combination of these conditions is (-∞,0)

The or combination of the solutions above is:

Solution: (-∞,0) U (4,∞)

Please log in or register to add a comment.