A.
There are 15 people in the chorus and each year the pepople increases by 3. Let t represent the number of years. Then each year the number of people is:
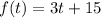
B.
There are 30 people in the band, each year the people increases by 2. Let t represent the number of years. Then each year the numbe of people in the band is:
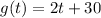
C.
After 9 years the number of people will be:
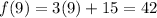
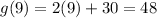
Therefore, after 9 years the chorus will have 42 people and the band will have 48 people.
D.
To find the number of years in which the number of people will be the same we equate the functions and solve for t:
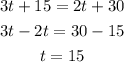
Therefore, after 15 years the band and chorus will have the same number of people.