We need to find x in term of j(x).
First, if we move -3 to the left hand side as +3, we have

By symmetry, we can write this result as

Now, we need to move the coefficient of x to the right hand side. This is given by
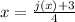
which can be rewritten as

which is the answer.