Question

the half-life of a radioactive kind of silver is 250 days. if you start with 960 grams of it, how much will be life after 500 days

Answer 1

This process can be modeled by the next formula:

`N(t)=N_0((1)/(2))^{\frac{t}{t_{1/2_{}_{}}}}`

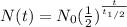
where N(t) is the quantity of the substance remaining, N0 is the initial quantity of the substance, t is the time elapsed, and t1/2 is the half-life of the substance.

Substituting with N0 = 960 grams, t = 500 days, and t1/2 = 250 days, we get:

`\begin{gathered} N(t)=960\cdot((1)/(2))^{(500)/(250)} \\ N(t)=960\cdot((1)/(2))^2 \\ N(t)=960\cdot(1)/(4) \\ N(t)=240\text{ grams} \end{gathered}`

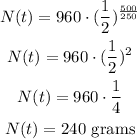
There will be 240 grams