line KP is the Diameter = 42
radius total = radius of the largest circle = diameter/2 = 42/2 = 21,
ON = NL = LK ........given from the question....we can represent this as x
that is,
x + x + x = radius total
3x = 21,
x = 21/3 = 7
That is, ON = NL = LK = 7
Now, radius small = radius of the smallest circle = ON = 7.
Let's calculate the Area of the largest circle...........
Area total = pi * radius total
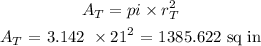
Let's calculate the Area of the smallest circle...........
Area small = pi * radius small
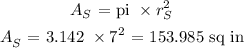
Now , to calculate the area of the shaded region, we have to substract the area of the smallest from the largest and divide the answer by 2
Area shaded = (1385.622 - 153.985) / 2 = 1231.664 / 2 = 615.832 = 616 sq in
That's all
Thank you!