The equation of the parabola is;
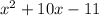
The general equation of a parabola is;
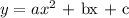
We have the axis of symmetry dividing the parabola into 2 equal halves
So, the distance from the axis of symmetry point to both roots are the same
So, the distance between - 5 and 1 is 1-(-5) = 6
This is the distance to the left
So, we need the distance to the right and that would be taking off 6 units from -5; so we have it as -11
So the equation is;
