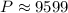Question

How many bacteria will there be?Round to the nearest whole number

Answer 1

You know that:

- She puts a population of 300 bacteria into a favorable growth medium at 8:00 A.M.

- At 5:00 P.M. the population is 1100 bacteria,

- The next morning, at 8:00 A.M. she comes back to the lab.

By definition, an Exponential Growth Model has the following form:

`P=P_0e^(rt)`

Where "r" is the growth rate (in decimal form), "t" is the number of times intervals and this is the initial amount:

`P_0`

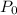
1. In this case, from 8:00 A.M to 5:00 P.M. you know that:

`\begin{gathered} P=1100 \\ t=9 \end{gathered}`

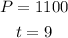
And the initial amount is:

`P_0=300`

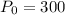
2. Then, you can substitute values into the equation and solve for "r", in order to find its value:

`\begin{gathered} P=P_0e^(rt) \\ \\ 1100=300\cdot_{}e^(r(9)) \end{gathered}`

`(1100)/(300)=e^(9r)`

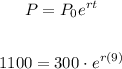
Remember the following properties:

`\begin{gathered} ln(a)^m=m\cdot\log (a)^{} \\ \\ \ln (e)=1 \end{gathered}`

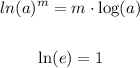
Then taking Natural Logarithm on both sides and simplifying, you get:

`\begin{gathered} \ln ((1100)/(300))=\ln (e)^(9r) \\ \\ \ln ((1100)/(300))=9r\cdot\ln (e) \\ \\ \ln ((1100)/(300))=9r(1) \\ \\ \ln ((1100)/(300))=9r \\ \\ (\ln ((1100)/(300)))/(9)=r \end{gathered}`

`r\approx0.1444`

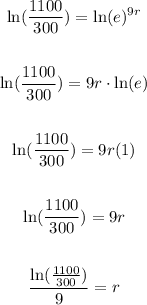
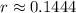
3. From 8:00 A.M. to 8:00 A.M in the next morning, there are 24 hours. Then, you can say that:

`\begin{gathered} P_0=300 \\ r\approx0.1444 \\ t=24 \end{gathered}`

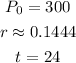
Now you can substitute values and find the number of bacteria at 8:00 A.M of the next morning:

`\begin{gathered} P=P_0e^(rt) \\ \\ P=300\cdot e^((0.1444)(24)) \\ \\ P=300\cdot e^((3.4656)) \end{gathered}`

`P\approx9599`

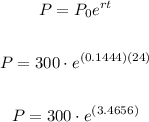
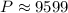
Hence, the answer is:

`P\approx9599`