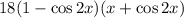Power reduction formulas for squares:
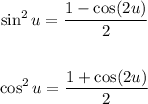
Given expression:
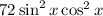
Use the reduction formula: For the given expression u is x:

Simplify:
-Multiply:
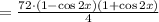
-Divide 72 into 4:
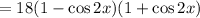
Then, an equivalent expression that does not contain powers of trigonometric functions greater than 1 is: