Help please:Suppose that x and y inversely, and x=10 when y=8 write the function that models the inverse variation

Question

asked Jul 20, 2023 217k views

1 Answer

Stuxen · Answer 1 · 2023-07-25T15:07:38+0000

SOLUTION

From the question, we are told that y varies inversely as x

This is mathematically written as

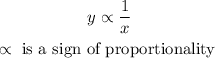
$\begin{gathered} y\propto(1)/(x) \\ \propto\text{ is a sign of proportionality } \end{gathered}$

Now, we will remove the proportionality sign and replace it with equal to sign =

If we do this, we will intoduce a constant k

$\begin{gathered} y\propto(1)/(x) \\ y=k*(1)/(x) \\ y=(k)/(x) \end{gathered}$

So we have the formula

We will substitute the values of x for 10 and y for 8 into the formula to get k, we have

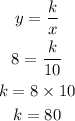
$\begin{gathered} y=(k)/(x) \\ 8=(k)/(10) \\ k=8*10 \\ k=80 \end{gathered}$

Now, we will substitute k for 80 back into the formula to get the inverse function, we have

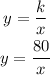
$\begin{gathered} y=(k)/(x) \\ y=(80)/(x) \end{gathered}$

Hence the answer is option C