Question

Help please:Suppose that x and y inversely, and x=10 when y=8 write the function that models the inverse variation

Answer 1

From the question, we are told that y varies inversely as x

This is mathematically written as

`\begin{gathered} y\propto(1)/(x) \\ \propto\text{ is a sign of proportionality } \end{gathered}`

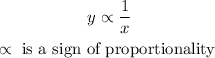
Now, we will remove the proportionality sign and replace it with equal to sign =

If we do this, we will intoduce a constant k

`\begin{gathered} y\propto(1)/(x) \\ y=k*(1)/(x) \\ y=(k)/(x) \end{gathered}`

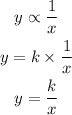
So we have the formula

`y=(k)/(x)`

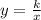
We will substitute the values of x for 10 and y for 8 into the formula to get k, we have

`\begin{gathered} y=(k)/(x) \\ 8=(k)/(10) \\ k=8*10 \\ k=80 \end{gathered}`

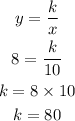
Now, we will substitute k for 80 back into the formula to get the inverse function, we have

`\begin{gathered} y=(k)/(x) \\ y=(80)/(x) \end{gathered}`

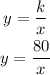
Hence the answer is option C