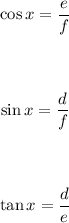1 Answer

Knagaev · Answer 1 · 2023-05-29T22:33:08+0000

Given the right traingle with side lengths:

d, e, and f

Let's find cosx, sinx, and tanx.

From the given figure, we have:

Opposite side which is the side opposite the given angle(x) = d

Adjacent side which is the side adjacent the given angle (x) = e

Hypotenuse which is the longest side of the triangle = f

θ which is the given angle = x

To solve this, we are to apply trigonometric ratio formula for each of the following.

Thus, we have:

• a) cos x:

Apply the trigonometric ratio formula for cosine:

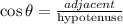
$\cos \theta=\frac{adjacent}{\text{hypotenuse}}$

Substitute the values into the equation:

$\cos x=(e)/(f)$

• b) sinx:

Apply the tigonometric ratio formula for sine:

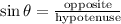
$\sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}$

Substitute the variables into the equation:

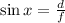
$\sin x=(d)/(f)$

• c) tanx:

Apply the trigonometric ratio formula for tan:

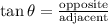
$\tan \theta=\frac{\text{opposite}}{\text{adjacent}}$

Substitute the variables into the equation:

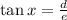
$\tan x=(d)/(e)$

ANSWER:

$\begin{gathered} \cos x=(e)/(f) \\ \\ \\ \sin x=(d)/(f) \\ \\ \\ \tan x=(d)/(e) \end{gathered}$

Please log in or register to add a comment.