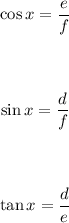Given the right traingle with side lengths:
d, e, and f
Let's find cosx, sinx, and tanx.
From the given figure, we have:
Opposite side which is the side opposite the given angle(x) = d
Adjacent side which is the side adjacent the given angle (x) = e
Hypotenuse which is the longest side of the triangle = f
θ which is the given angle = x
To solve this, we are to apply trigonometric ratio formula for each of the following.
Thus, we have:
• a) cos x:
Apply the trigonometric ratio formula for cosine:
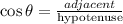
Substitute the values into the equation:
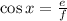
• b) sinx:
Apply the tigonometric ratio formula for sine:
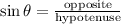
Substitute the variables into the equation:
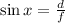
• c) tanx:
Apply the trigonometric ratio formula for tan:
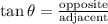
Substitute the variables into the equation:
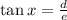
ANSWER: