Question

(a) . what is the kinetic energy in joules of a 1000 kg automobile traveling and 90 km/h(b) . how much work would have to be done to bring a 1000 kg automobile traveling at 90 km/h to a stop

Answer 1

Part (a)

Given data:

Mass of the automobile;

`m=1000\text{ kg}`

Velocity of the automobile;

`v=90\text{ km/h}`

Converting the velocity from km/h to m/s:

`\begin{gathered} v=90\text{ km/h}*\frac{1000\text{ m}}{3600\text{ s}} \\ =25\text{ m/s} \end{gathered}`

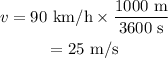
The kinetic energy of the automobile is given as,

`K\mathrm{}E=(1)/(2)mv^2`

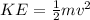
Substituting all known values,

`\begin{gathered} KE=(1)/(2)*(1000\text{ kg})*(25\text{ m/s})^2 \\ =312500\text{ J } \end{gathered}`

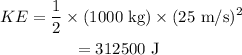
Therefore, kinetic energy of the automobile is 312500 J.

Part (b)

When the automobile is stoped, its velocity becomes 0 i.e. v'=0. Therefore, kinetic energy of the automobile when it comes to stop is given as,

`\begin{gathered} K\mathrm{}E^(\prime)=(1)/(2)mv^(\prime2) \\ =(1)/(2)*(1000\text{ kg})*(0\text{ m/s})^2 \\ =0\text{ J} \end{gathered}`

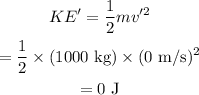
According to work-energy theorem, the work is equal to change in kinetic energy. Therefore,

`W=K\mathrm{}E^(\prime)-K\mathrm{}E\text{. }`

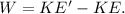
Substituting all known values,

`\begin{gathered} W=0\text{ J}-312500\text{ J} \\ =-312500\text{ J} \end{gathered}`

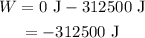
Here, negative sign indicates that the work is done on the system.

Therefore, the work done to bring the automobile to stop is 312500 J.