Part (a)
Given data:
Mass of the automobile;
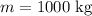
Velocity of the automobile;
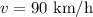
Converting the velocity from km/h to m/s:
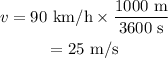
The kinetic energy of the automobile is given as,
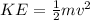
Substituting all known values,
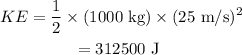
Therefore, kinetic energy of the automobile is 312500 J.
Part (b)
When the automobile is stoped, its velocity becomes 0 i.e. v'=0. Therefore, kinetic energy of the automobile when it comes to stop is given as,
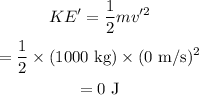
According to work-energy theorem, the work is equal to change in kinetic energy. Therefore,
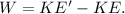
Substituting all known values,
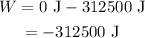
Here, negative sign indicates that the work is done on the system.
Therefore, the work done to bring the automobile to stop is 312500 J.