Given the function:
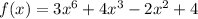
Let's use the rational zeros theorem to state all the possible zeros of the function.
Every zero of the function will have the form:

Where:
p is a factor of the last term(constant)
q is a factor of the leading coefficient.
Where:
Leading coefficient, q = 3
Factors of 3 = ±1, ±3
Constant term, p = 4
Factors of 4 = ±1, ±2, ±4
![\begin{gathered} (p)/(q)=±(1)/(1),\pm(1)/(3),\operatorname{\pm}(2)/(1),\operatorname{\pm}(2)/(3),\operatorname{\pm}(4)/(1),\operatorname{\pm}(4)/(3) \\ \\ Now\text{ simplify:} \\ (p)/(q)=\operatorname{\pm}1,\operatorname{\pm}(1)/(3),\operatorname{\pm}2,\operatorname{\pm}(2)/(3),\operatorname{\pm}4,\operatorname{\pm}(4)/(3) \end{gathered}]()
Therefore, the possible zeros of the polynomial are:
![\pm1,\operatorname{\pm}(1)/(3),\operatorname{\pm}2,\operatorname{\pm}(2)/(3),\operatorname{\pm}4,\operatorname{\pm}(4)/(3)]()
ANSWER:
![\pm1,\operatorname{\pm}(1)/(3),\operatorname{\pm}2,\operatorname{\pm}(2)/(3),\operatorname{\pm}4,\operatorname{\pm}(4)/(3)]()