For this problem, we are given the perimeter of a rectangle and a relation between the width and the length. We need to determine the width.
The perimeter of a rectangle is given by:
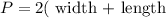
Therefore, we have:
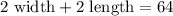
We know that the width is 6 centimeters less than the length, therefore we can write the expression below:
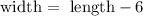
If we replace the expression above on the second one, we have:

We can use this value to find the width, which is:
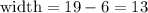
The width is equal to 13 cm.