Given the Quadratic Equation:
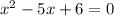
1. Find the x-intercepts:
- Factor the equation by finding two numbers whose sum is -5 and whose product is 6. These are -2 and -3, because:
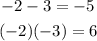
Then:
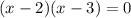
- Now you know that the x-intercepts are:
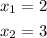
2. Now you need to graph this function:
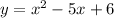
In order to find the graph with better precision, you can find the vertex:
- Find the x-coordinate with this formula:
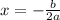
In this case, knowing that the function has the form:
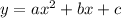
You can identify that:
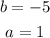
Then, you get:
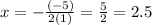
- Find the y-coordinate of the vertex by substituting the x-coordinate into the function and evaluating:
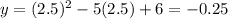
Hence, the vertex of the parabola is:
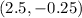
3. To find two other points on the parabola, you can substitute these values into the function and evaluate:
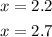
Then, you get:
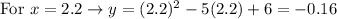
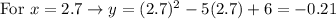
Therefore, you know these two other points:
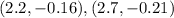
Hence, the answer is: