Question

8) Find the perimeter of PQR with vertices P(-3, 3), Q(2, 3), and R(2,-6).

Answer 1

We have the following triangle:

In order to find the perimeter, we need to find the distances between each pair of points. The distance formula between 2 points is:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

where the coordinates of the 2 points are:

`\begin{gathered} (x_1,y_1) \\ \text{and} \\ (x_2,y_2) \end{gathered}`

Lets apply this formula to the points P and Q. In this case, we have

`d_(PQ)=\sqrt[]{(-3-2)^2+(3-3)^2}`

which gives

`d_(PQ)=\sqrt[]{25}=5`

Now, for the points QR, the distance is

`d_(QR)=\sqrt[]{(2-2)^2+(-6-3)^2}`

which gives

`d_(QR)=\sqrt[]{81}=9`

and finally, lest obtain the distance between P and R:

`d_(PR)=\sqrt[]{(2-(-3))^2+\mleft(-6-3\mright)^2}`

which gives

`\begin{gathered} d_(PR)=\sqrt[]{5^2+9^2} \\ d_(PR)=\sqrt[]{106} \\ d_(PR)=10.2956 \end{gathered}`

Then, the perimeter P is given by

`\begin{gathered} P=d_(PQ)+d_(QR)+d_(PR) \\ P=5+9+10.2956 \\ P=24.2956 \end{gathered}`

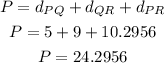
that is, the perimeter is equal to 24.2956 units