We have the following triangle:
In order to find the perimeter, we need to find the distances between each pair of points. The distance formula between 2 points is:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
where the coordinates of the 2 points are:
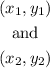
Lets apply this formula to the points P and Q. In this case, we have
![d_(PQ)=\sqrt[]{(-3-2)^2+(3-3)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/wr407am6re85d7m8lmnz1l9x2bdpz3n31j.png)
which gives
![d_(PQ)=\sqrt[]{25}=5](https://img.qammunity.org/2023/formulas/mathematics/college/3w2vopvekhyzv8cquxc3gwigpcxwlnz43k.png)
Now, for the points QR, the distance is
![d_(QR)=\sqrt[]{(2-2)^2+(-6-3)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/f1m12lhp4u8ovhmtmqt4vf47s13lzvymig.png)
which gives
![d_(QR)=\sqrt[]{81}=9](https://img.qammunity.org/2023/formulas/mathematics/college/5l7chapzgerl2pcw429ly6izlijed9kiik.png)
and finally, lest obtain the distance between P and R:
![d_(PR)=\sqrt[]{(2-(-3))^2+\mleft(-6-3\mright)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1kc40yfczrug6jjtkuwgpqq6j2rf2ahjcl.png)
which gives
![\begin{gathered} d_(PR)=\sqrt[]{5^2+9^2} \\ d_(PR)=\sqrt[]{106} \\ d_(PR)=10.2956 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/69ydxivmnpqbv8sixpm039a6b2jkbso898.png)
Then, the perimeter P is given by
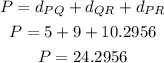
that is, the perimeter is equal to 24.2956 units