Question

The graph to the right shows the relationship between distance and time for a car that is similar to constant speed. 1) What is the velocity ?_______________ 2) Is it a function ________ 3) If it is a function, write the rule to represent it ___________ 4.) Make a table for the function, and indicate 6 pairs of inputs / outputs

Answer 1

1)

In order to find the velocity, we just need to divide a distance by the corresponding time.

So, using the point (2, 120), that is, a distance of 120 for a time of 2, we have:

`\text{velocity}=(120)/(2)=60`

2)

Is it a function? Yes, since each value in the x-axis has only one corresponding value in the y-axis.

3)

To find the rule of this function, we can use the slope-intercept of the linear function (y = mx + b) and two points of the graph, for example (0, 0) and (2, 120), so we have:

`\begin{gathered} y=mx+b \\ (0,0)\colon \\ 0=0m+b\to b=0 \\ \\ (2,120) \\ 120=2m+b \\ 2m=120 \\ m=60 \end{gathered}`

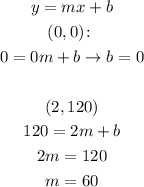
So our function is y = 60x

4)

Using the rule we found, we can write the table: